SDS FFT performance on low frequency signals
May 23, 2018
Like many modern oscilloscopes, the SIGLENT SDS series feature FFT math functions that calculate frequency information from the acquired voltage vs. time data. FFT stands for Fast Fourier Transform, and is a common method for determining the frequency content of a time-varying signal. Converting time domain data to the frequency domain makes measuring characteristics like phase noise and harmonics much easier. Oscilloscopes don’t have the dynamic range or sensitivity of a true spectrum analyzer, but these new designs can provide a fine level of detail that may be just enough for your application.
FFTs are commonly used on high frequencies, but they can also be used on signals with fairly low frequencies.
In this note, I am going to show the FFT performance of two series of our scopes by sourcing a 10 mHz (100 s period), 10 Vpp sine wave using a SIGLENT SDG805 Function Generator into Channel 1.
For those interested, here are the specs for the SDG805
SDS1000X/SDS2000X Series:
The SDS1000X and 2000X series feature an FFT function that uses up to 16 kpts of timebase data to calculate the frequency data and a timebase maximum of 50 s/div.
Here are the FFT results with the available window settings for a 10 mHz sinewave –
The scope can show a split timebase and FFT view:
For the rest, I will use the exclusive FFT view.
Rectangle
Blackman
Hanning
Hamming
Flat Top
SDS1000X-E Series:
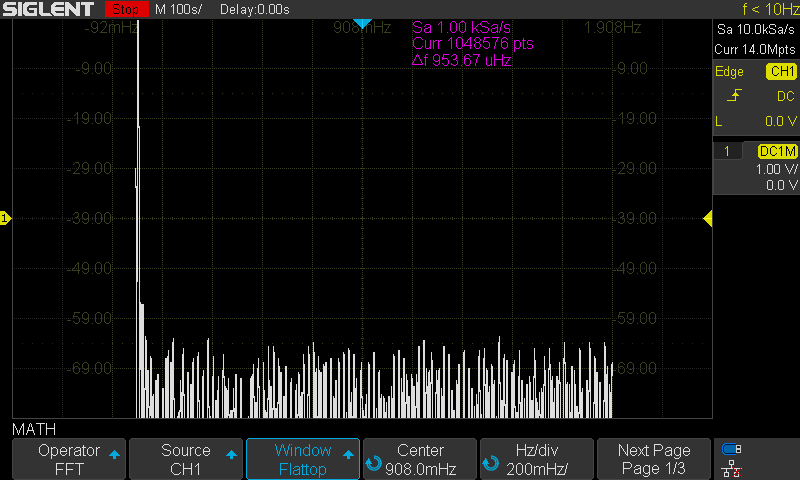
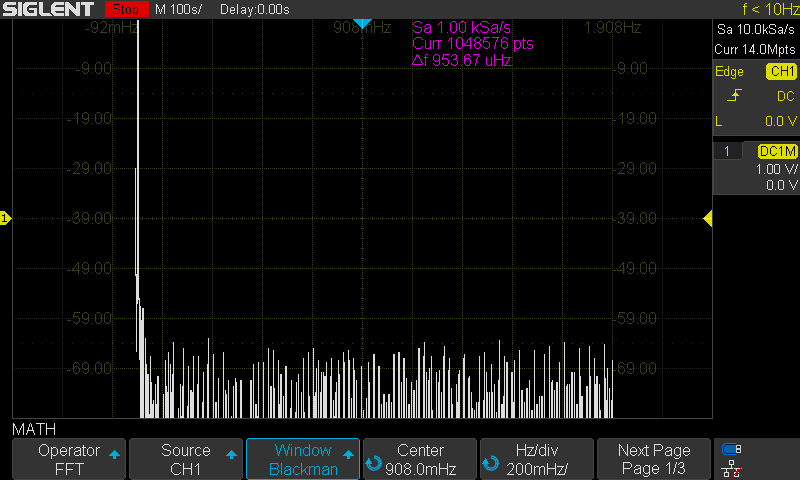
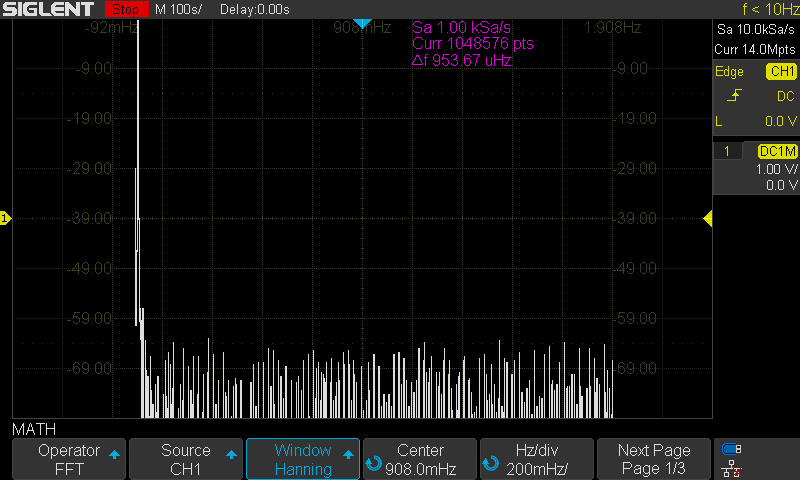
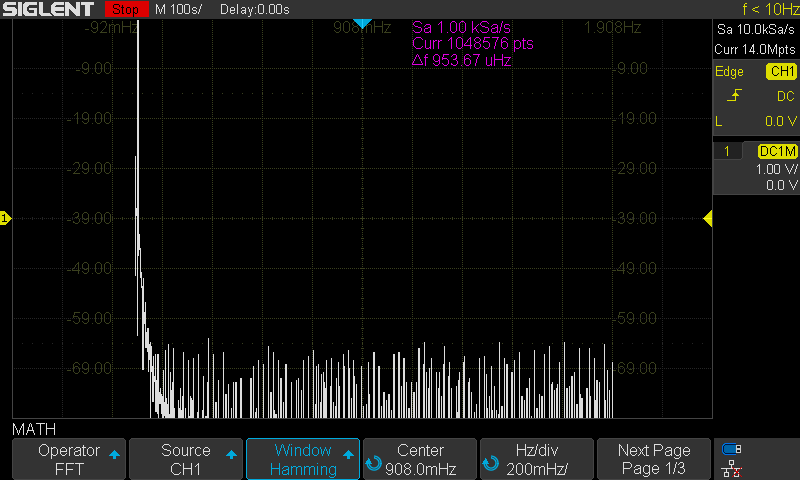
The SDS1000X-E series feature a new math co-processor that increases the maximum data depth of the FFT function to 1 Mpts. They also feature a timebase maximum of 100 s/div. These increases allow the X-E to have much finer timebase detail and to acquire useful data for even lower frequencies than many scopes on the market.
Here are the FFT results with the available window settings for a 10 mHz sinewave –
The scope can show a split timebase and FFT view:
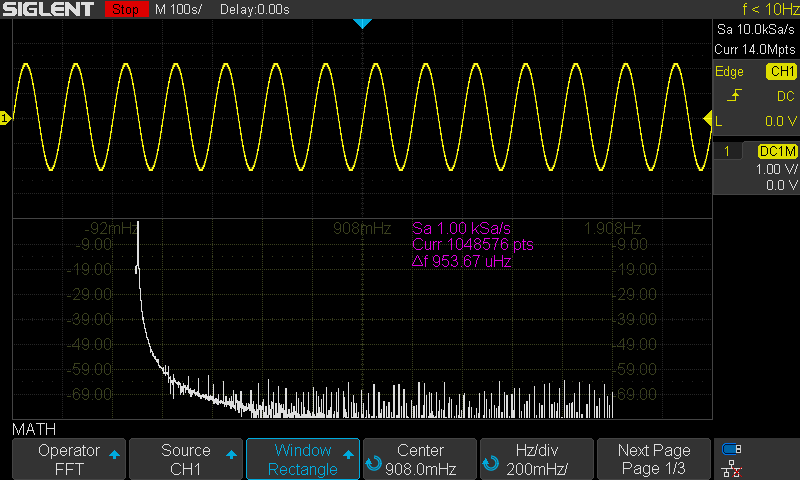
For the rest, I will use the exclusive FFT view.
Rectangle
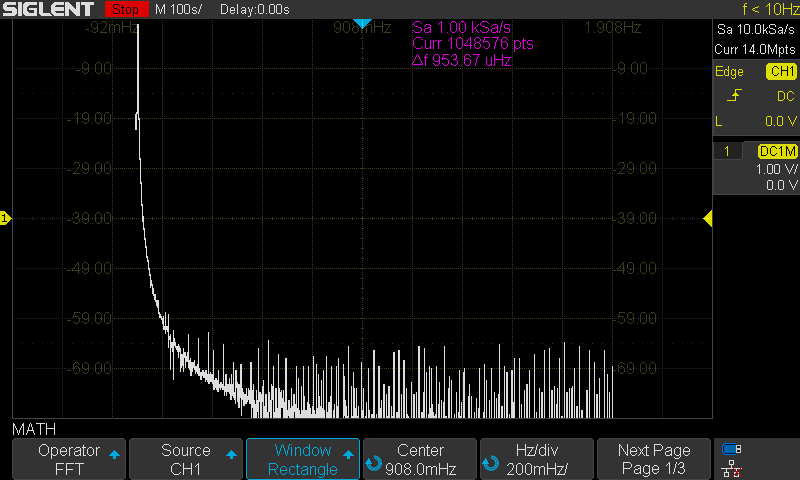
Blackman
Hanning
Hamming
Flat Top